量子自旋液体是一种即使在零温下也不会发生对称性自发破缺的量子物质形态，其基本概念最早由诺贝尔获得者P. W. Anderson在1973年提出。之后，人们尝试利用自旋液体来解释高温超导的现象。近年来，随着实验上大量阻挫量子自旋材料的出现，找到具有自旋液体基态的材料变得越来越有可能。从实验和理论两个方面，量子自旋液体已成为凝聚态物理学量子多体问题研究的一个热点方向。

Kagome晶格作为一种强阻挫晶格，是实现量子自旋液体的理想模型。但对于一般的反铁磁海森堡模型，由于存在符号问题，人们无法利用量子蒙特卡洛方法数值研究系统基态的行为。2002年，Balents、Fisher和Girvin三位物理学家提出的所谓的BFG模型是一类可以实现量子自旋液体的模型，且该模型没有符号问题，可以展开大规模的量子蒙特卡洛研究，人们对于该模型取得了很多研究成果，尤其是零磁矩的情况。但如果对该模型加上一个Zeeman场，调节至1/6平均磁矩的时候，该系统是量子自旋液体，还是对称性破缺的条纹固体序，尚存在争议。

近期，中国科学院物理研究所/北京凝聚态物理国家研究中心博士后王艳成（已出站，现任教于中国矿业大学）、副研究员孟子杨，与重庆大学研究员张学锋、德国马普学会教授Frank Pollmann、耶鲁大学助理教授程蒙等组成的研究团队，利用大规模的量子蒙特卡洛数值方法对基于BFG模型的阻挫磁性系统在1/6平均磁矩下的情况展开了细致的研究，给出了该模型的详细相图，从理论和数值上证实存在一种新的超越Lieb- Schultz-Mattis-Oshikawa-Hastings（LSMOH）理论框架的量子自旋液体，其性质可用偶数伊辛规范场理论描述。

计算发现，该量子自旋液体到铁磁序的相变行为属于自旋子（spinon）凝聚有关的一类特殊的三维\(XY^{*}\)相变普适类。该研究扩展了Kagome晶格上可能存在的量子自旋液体基态的范围，且这种超越LSMOH理论预言的量子自旋液体通往其他对称性破缺相的相变过程对应于新型分数化任意子（anyon）凝聚，扩展了人们对于任意子凝聚行为的理解。

相关研究成果发表在《物理评论快报》上。该研究得到了国家重点研发计划、国家自然科学基金、中科院战略性先导科技专项培育项目的资助。量子蒙特卡洛模拟所需的大规模的并行计算在物理所量子模拟科学中心和天津国家超算中心天河1号平台上完成，计算过程中得到了天津国家超算中心博士孟祥飞、工程师赵洋等的支持。

论文链接：

https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.121.057202

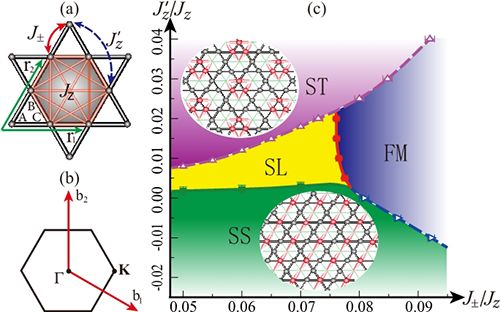
图1.（a）Kagome晶格以及不同格点间的自旋相互作用；（b）Kagome晶格的倒格矢及其第一布里渊区；（c）扩展BFG模型在1/6 平均磁矩下的相图。ST（staggered solid）：交错固体相，SS（stripped solid）：条纹固体相，FM (ferromagnet)：铁磁相，SL(quantum spin liquid）：量子自旋液体相。

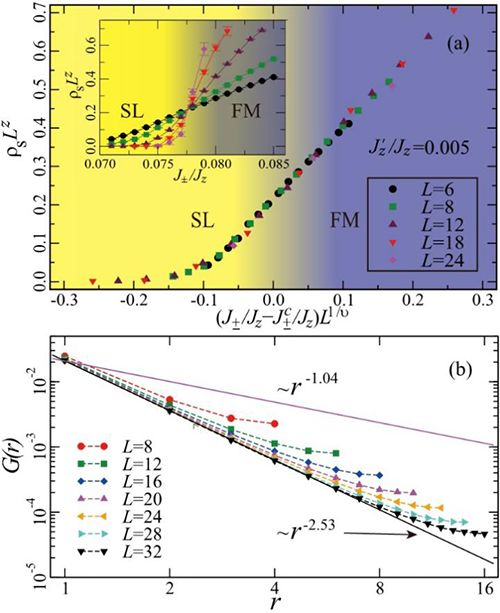
图2。（a）自旋刚度（spin stiffness）在自旋液体（SL）到铁磁序（FM）相变点附近的数据跌落，其中，临界指数 υ 是三维XY普适类的临界指数；（b）等时自旋-自旋关联函数\(G(r)=\left \langle S_{0}^{+}S_{r}^{-} \right \rangle\)随距离 r 的变化关系。在双对数坐标下，\(G(r)\sim r^{-(1+\eta )}\)，其中反常维度 η=1.53(4)，远大于普通的三维 XY 的反常维度0.04。因此该相变属于一类特殊的三维\(XY^{*}\)普适类。