近年来，量子安全成为信息安全研究的热点和产业界关注的新一轮投入重点。原因也非常显而易见，密码是信息安全的底线，如果底线要被突破了，之前设置的防线再纵深、再综合恐怕也都沦为了摆设。所以量子安全是信息安全发展里程中的大事件和大趋势。中国信息协会量子信息分会顾问专家孙林红老师从事密码理论和攻防研究多年，近来对量子安全密码技术从科学和发展的角度进行了梳理。我们在此特将孙老师的有关观点和报告尽可能通俗化的整理编辑为系列文章供各位读者朋友交流研讨。

上期我们从陷门开始去讲述密码和密码安全性，没有陷门做不出密码，有了陷门又可能引入不安全性，现代密码的复杂性在此显露无疑。由此，人们希望依靠数学，花了很多年也花了很大力气去研究可证明安全的公钥密码。基于数学的密码算法是越复杂就越安全吗？在第二次量子科技革命到来的情况下，这条道路是否还有效呢？

1、量子计算攻击效果犀利著名的Shor算法能用于质因数分解，我们就从基于Shor算法的量子计算攻击这一角度去阐述量子计算攻击到底厉害在哪。要理解Shor算法，需要首先从傅里叶变换说起。傅里叶变换是通过一组特殊的正交基来实现时域到频域的变换，把时域序列转换到频域上以刻画其变化规律，从而给人们提供了一个新的审视世界的角度，也为处理信号、生成信号和传输信号提供了关键的工具。当前我们在信息通信技术中通常使用的是快速傅里叶变换（Fast Fourier Transform, FFT），它是信息时代数据处理无处不在的基本工具。量子傅里叶变换（Quantum Fourier Transform, QFT）是在量子计算机上进行傅里叶变换计算。我们知道量子计算与经典计算有本质上的不同，虽然现有量子算法无论是功能还是数量还很有限，但量子计算“恰恰”适用于执行傅里叶变换。第一，基于量子相干性，QFT通过构造合适的量子线路，对时域上有限长序列通过量子线路输入端形成的量子态进行测量，就可以高概率测出频域上体现的特征规律。第二，基于量子叠加性，QFT算法处理单个数据流的速度虽然与经典FFT相同，但由于量子计算机允许一组量子比特同时对多种信息状态进行编码，可以一次将所有输入计算完成，由于QFT具有这样同时处理多个数据流的能力，因此它比FFT快得多。简而言之QFT比之FFT来说是殊途同归又远胜于斯。1994年Peter Shor设计了Shor算法，它比以往任何经典算法都能更快速有效的进行质因数分解。Shor算法的中心子程序和其效率来源就是量子傅里叶变换，从实践效果分析，Shor量子算法比经典算法有指数级的加速效果。例如：分解一个400位的大整数，经典计算机约需要5×10²²次操作，而量子计算机约需要6×10⁷次操作，量子计算机所需操作数仅为经典计算机的80万亿分之一。使用Shor算法解质因数分解问题的优势是能以多项式时间解出分解整数n：也就是说它需要的时间是log n的某个多项式这么长（注意这里log n的意义恰好对应的是输入数字的二进制序列长度）。更精确的说，这个算法花费O(n³ log n)的时间。比传统已知最快的因数分解算法——普通数域筛选法快出了指数级差异。因此我们说Shor量子算法可以在多项式时间内解决大整数分解和离散对数求解等复杂数学问题，从而可以对广泛使用的RSA、ECC、DSA、ElGamal等公钥密码算法进行快速破解。                                              

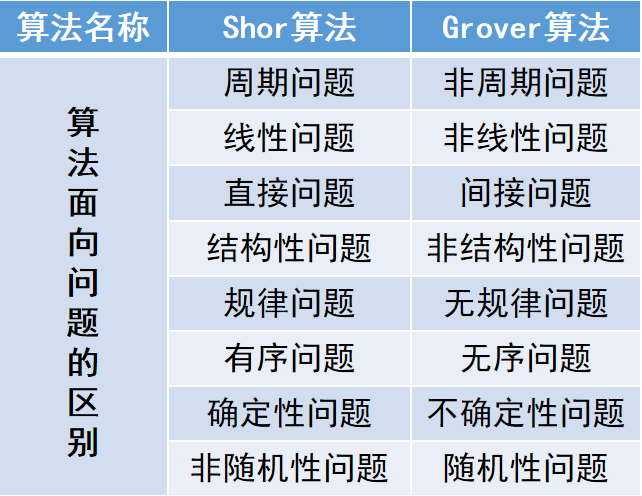
除Shor算法外，基于其它量子算法也能攻击现用密码。1997年Lov Grover发明的Grover量子算法，也称为量子快速搜寻算法，它能从大量未分类的无序个体中快速寻找出某个特定的个体。Grover算法先控制量子线路重复进行某些操作来改变待输出的量，使它刚好等于目标的概率增加到接近1，再测量获得输出态。它能够将非结构化数据或无序数据库的搜索时间降为经典算法的平方根时间。尽管设计良好的对称密码算法不存在明显的数学结构，基于Grover算法的这种能力，仍然可以对这种“弱结构”进行挖掘从而破解对称密码，甚至可以直接从所有可能的密钥中暴力破解寻找到正确密钥。以这两种典型的量子算法为例，在下图中列表展示其各自面向的求解问题特征。

2、经典密码安全堪忧人们讨论安全时常使用木桶理论，那量子算法的攻击导致经典密码安全的到底哪些部位、哪些环节需要重新评估呢？对基于数学的密码算法来说，安全假设、攻击模型等这些讨论安全时的“前提”还是固定的，现在也没有发生什么变化，也就是前提条件稳定。为了“有理可依”，而不是在算法安全性上“说不清”，人们设计的可证明安全理论也是有清晰的逻辑，无论是过程和结果，它都可说是逻辑严谨、结果确切的，这些都没有变化。变化量在于可证明安全公钥密码的出发点在于在一个大的代数空间中去隐藏结构（从上期内容我们知道首先作为可用的公钥算法它必然存在陷门就是存在结构），而Shor算法从原理上擅长的就是快速寻找出来这个结构，它深刻地揭示了在量子计算环境下是很难隐藏结构的。原来依托数学难题构造的密码算法（如RSA、DSA、ECCDSA等）本身不安全了，一旦有中等规模以上的通用性量子计算机出现，运行Shor算法就可以在可接受的时间内直接破解当前广泛使用的RSA、ECC等公钥加密算法。2021年法国研究者发布的研究成果表明，通过将量子存储器集成到量子计算机中，13436个量子比特耗费177天即可破解RSA-2048。基于数学的现代密码算法设计的根本原则是唯难不破、唯计算复杂度不破。算法足够难、计算复杂度足够高才能不被破解。上期内容我们已经说了，除了基于可证明困难问题的公钥密码外，还有一类以计算复杂度（主要是时间计算复杂度）为衡量准则的启发式安全密码。启发式安全的分组密码、序列密码、杂凑函数等由于原理的不同，其抗量子计算的能力有细微的差别，下面分别进行阐述。

总体上看，启发式安全对称密码也面临量子计算的风险，但由于对称密码算法一般不存在明显的数学结构，这种风险相对还较小。使用Shor算法挖掘对称密码算法的弱结构的成功概率和效率不如对公钥密码那样高。也就是一般情况下经过量子傅里叶变换输出后的规律比较微弱、不够显著，无法高概率测量。但如果通过对对称密码进行分析掌握一定的规律，依此进行针对性预处理再使用Shor算法，这种经典—量子混合的量子攻击可能成功概率更高。还需要注意其它量子算法如Grover算法也可能对对称密码实施量子计算攻击。对称密码如何抵御这些量子攻击呢？密码学家提出的解决方案就是增加密钥长度或增加算法密文输出长度。

对序列密码来说，一般情况下经过量子傅里叶变换输出后的规律会更微弱、更不够显著，所以更无法高概率测量。但如果对序列密码算法进行深入的分析，能掌握一定的规律，则对上述量子计算攻击有帮助。

对杂凑密码来说，一般情况下经过量子傅里叶变换输出后的规律会进一步更微弱和不够显著，所以也无法高概率测量。但如果对杂凑函数算法进行深入的分析，能掌握一定的规律，则对上述量子计算攻击有帮助。
3、PQC算法的抗攻击能力到底如何？恐怕还无定论本期最后部分，专门讨论PQC算法的抗攻击能力。PQC算法是近年来被广泛关注的旨在抵御已知量子计算攻击的多类基于数学难题的密码技术，目标是能替代现用公钥密码。PQC的典型代表是NIST公钥密码算法征集入选的各类算法。那么它的抵抗能力到底如何？现在下结论恐怕为时尚早。PQC作为新公钥算法，其安全性的评估是个复杂的问题：例如，PQC算法同样也必须具备陷门；PQC的抗量子计算攻击指抵御已知量子计算攻击，未来可能有新形式的量子攻击出现；PQC基于的难题虽然是量子安全的，但在具体的算法中需要变通和退化，导致数学难题和密码算法的计算复杂度不能等价；为了抗量子攻击，PQC设计上还可能“顾此失彼”即被有针对性的传统算法破解。读者可能已经注意到，近一年来已经有多个PQC算法被传统方法破解的案例。2022年2月，IBM的专家发表论文宣称基于多变量密码（MQ）的Rainbow签名算法在其算法参数为安全等级为1的情况下，被一台笔记本电脑用53小时运行经典算法成功破解。2022年4月，以色列军方又发布了一份技术报告《错误学习问题（LWE）的安全性报告：改进的对偶格攻击方法》，基于经典算法的改进成功地实现了对格密码中LWE算法的攻击。受影响包括上述PQC标准筛选过程入选算法中的3个算法(Kyber、Saber和Dilithium)。

本期结语：量子安全时代，可证明安全的公钥密码是否存在成为了一个问题，也就是它面临的量子计算攻击风险最高、最容易被攻破；其它各类密码中，属于启发式安全范畴的对称密码面临的量子计算攻击风险相对低，但也可能被攻破（换句话说，对称密码安全性比更复杂的公钥密码强）；PQC的道路是延续传统安全上唯基于数学的计算复杂度不破原则的探寻，抗攻击能力如何目前还有待理论保证或充分的实践结论。已是临近年底，下期我们就总结回顾一年以来量子安全领域发展的主要动向。