我们在前面的文章中已经多次提到了量子电路，但并未多做解释，这次简单地介绍一下。

经典计算机发展过程中曾经出现过多种计算模型，影响最广的可能是图灵机模型，而现代计算机实际采用的是冯·诺依曼架构。

量子计算发展早期人们也曾仿照图灵机构想过量子图灵机，但并没有被广泛采纳。现在广泛使用的是多伊奇1989年推广经典的数字逻辑电路而提出的量子电路模型。

有些同行可能更喜欢叫它量子线路，但为了体现其渊源，我们还是称之为量子电路。

量子比特

人们在70年代曾经试图引入随机性来改进图灵机的效率。在数据层次上，这相当于引入比特的概率态（下图中轴线）：                                              

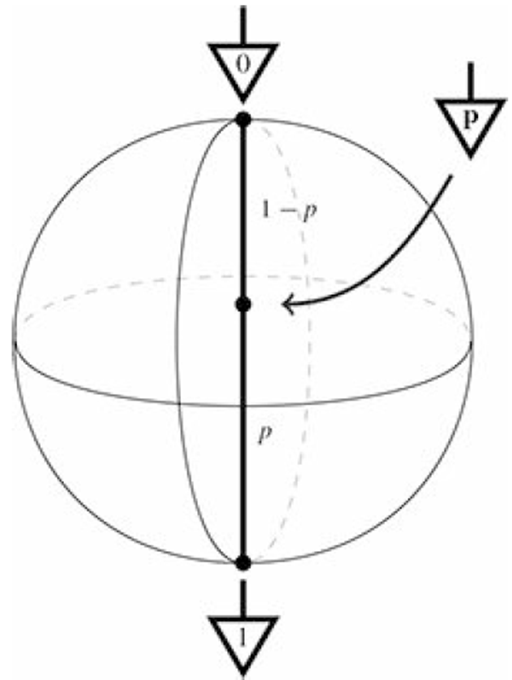
概率比特态 来源：“Picturing Quantum Processes”

但是因为总概率为1，我们并不能同时独立地操控0和1。现在我们试着将这里的概率态在复数上开平方，就可以形式上得到所谓的量子比特态和相应的概率幅：

而概率幅满足总概率为1的限制：

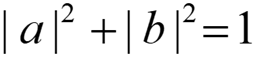
此时所有可能的态可以用一个球面来表示，我们叫它Bloch球面：

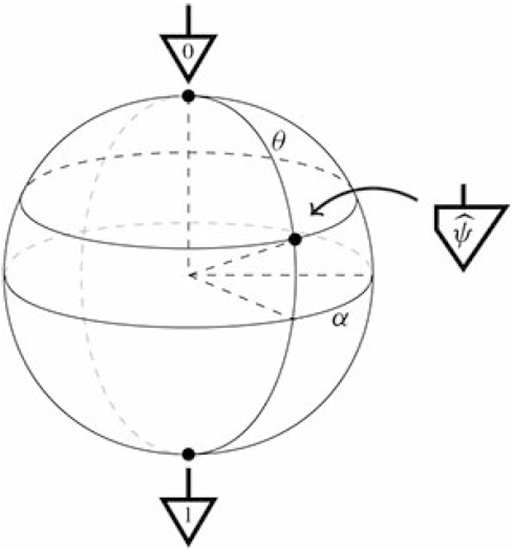
量子比特态 来源：“Picturing Quantum Processes”

注意此时的概率幅a和b在一定程度上是相互独立的。这就使得我们可以同时独立地操控|0>态和|1>态，从而有可能实现计算效率的飞跃。

我们的宏观世界当然并不是量子的。所以当我们读取量子比特时，它会坍缩回经典的概率态并丢失部分信息：

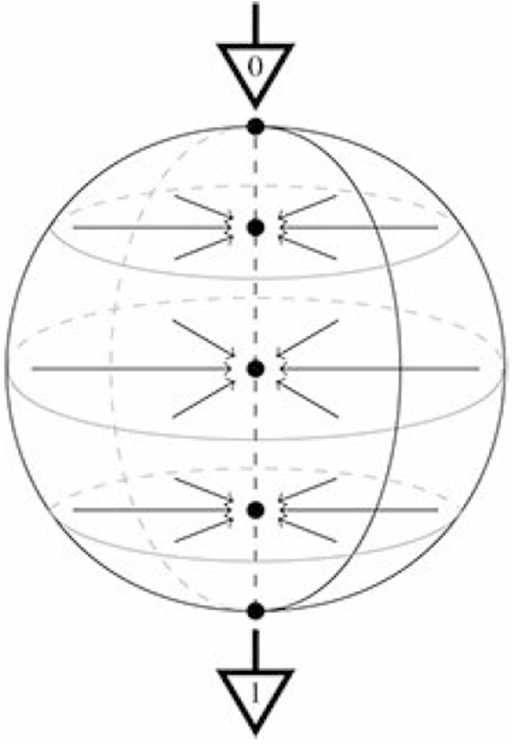
量子坍缩 来源：“Picturing Quantum Processes”

这便给量子计算的实现带来了一定的困难。

单比特门

经典比特只有0和1两种取值，所以我们只需要非门就可以遍历。

量子比特态覆盖了整个Bloch球面，因而是不可数的。如果我们只选择有限的门集，反复作用也只能得到可数多个态，不可能遍历整个球面。

于是我们退而求其次，希望找到有限门集，使得反复作用可以逼近任意态，就好比我们能用有理数逼近任意实数。

首先，我们注意到，从Bloch球面的角度来看，其实|0>和|1>取在哪个坐标轴上应该都可以：

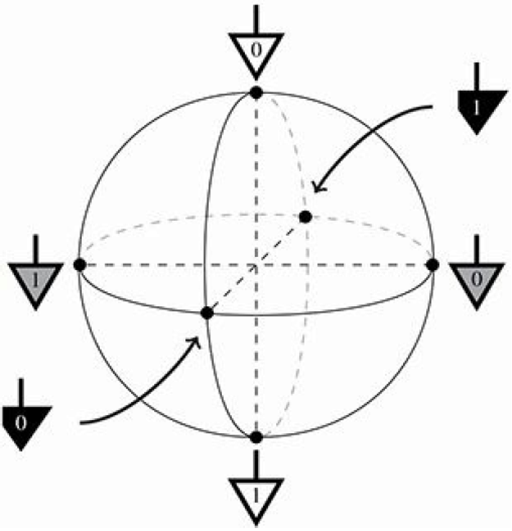
不同基 来源：“Picturing Quantum Processes”

所以我们首先来看怎么遍历这六个点。

我们可以通过绕y轴转 π/2角度将z轴转到x轴。但人们通常在这个转动上复合一个绕x轴的π角转动，并把它叫做阿达马（Hadamard）门，简称H门，见下图。

这样做的好处是两次作用H门就还原了，即H²=I。

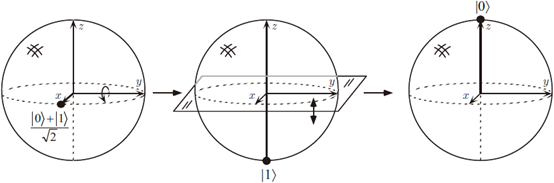
H门 来源：“Quantum Compotation and Quantum Information”

此外，为了在x轴和y轴之间切换，我们引入绕z轴的π/2角度转动，这就是相位门，也叫S门。

有了H门和S门，我们可以遍历坐标轴上的六个态了，但同时我们也被困在了其中：无论我们怎么反复作用也逃不出去。

如果把这六个态用线连起来，会形成下面的八面体：

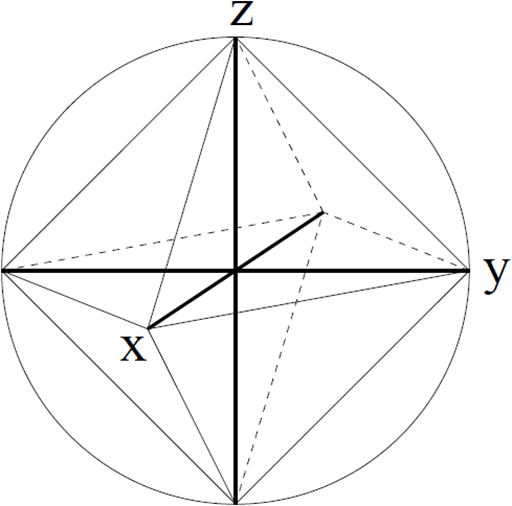
准经典八面体 来源：quant-ph/0403025

我们可以把这个八面体看成前面的概率态的某种推广。事实上，整个八面体中的态都无法超出概率型经典计算的范畴，尽管其中某些态存在量子叠加。因此，有朋友戏称其是“没有量子灵魂的”。

不过幸运的是，我们只需要想办法到达球面上这六个点外的某一点，那么就可以通过反复作用逼近任何一点了。例如，我们可以把这个点选成八面体对称轴与球面的交点：

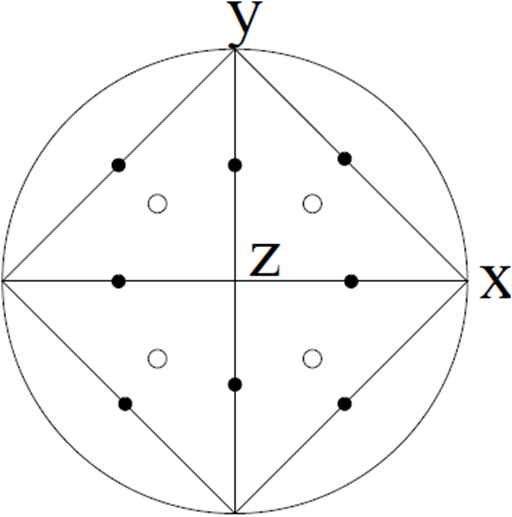
准经典八面体的俯视图，空心圈和实心圈分别代表穿过面和边的对称轴 来源：quant-ph/0403025

从门的角度来看，一个最直接的选择是让转角偏离π/2的倍数，例如π/4角度转动。

人们通常选择绕z轴的π/4角度转动，并称之为π/8门。这个命名看起来有点古怪，只是历史原因而已。π/8门又被称为T门。于是我们的结论是，反复作用H,S,T门可以逼近Bloch球面上的任意态。

怎么证明这一点呢？我们给一个简单的图像。

首先，单纯重复T门是不行的，因为π/4的8倍就变成了2π。我们需要把这些门组合出一个特殊的转动来，使得转角除以2π是无理数。为此，我们先类似于T门构建类似的Tx，也就是绕x轴的π/4转动：

T_x=HTH.

接着，我们先后作用T_x和T，会得到一个奇怪的转动R₁。首先R₁的转轴并不在坐标轴上。其次，R₁的转角θ由下式决定：

cos(θ/2)=cos²(π/8).

不难证明θ是2π的无理数倍（不过我还没去细读证明过程）。于是R₁的反复作用可以逼近一个大圆上的所有点。

进一步定义R₂=HR₁H以改变转轴，反复作用R₂得到的点可以密布另一个大圆。那么同时反复作用R₁和R₂呢？当然是近似得到整个Bloch球面。

这么做的代价是多少呢？也就是说，要以一定精度逼近一个任意的单比特门，需要大概多少个基础的H，S和T门呢？

先考虑一个大圆的情形，此时反复作用R₁得到的态在圆上差不多是均匀分布的。

假定我们需要的精度是ϵ。那么我们可以把圆分成1/ϵ份，必然有一份包含了需要的态。所以我们需要的基础门数目大概是Θ(1/ϵ)（Θ指的是相差常数因子的意义上等同）。同时考虑两个大圆只会让这个数目乘以一定的倍数，所以仍然是Θ(1/ϵ)。

以此类推，当我们的电路由m个任意单比特门组成时，如果我们仍然希望以精度ϵ去逼近它，需要的基础门的总数目大约是Θ(m²/ϵ)，因为这时候单个门的精度需要达到ϵ/m。

如果从P与NP的角度来看，这个代价当然不算高。但是，Solovay与Kitaev告诉我们，可以大幅降低这一代价。他们用到的技术可以称为级联（concatenation）。

简单地说，就是逐步地缩减与目标态的距离，而不是一步到位，如下图：

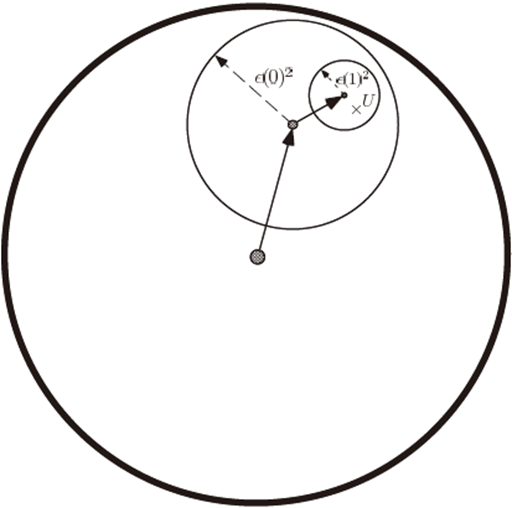
Solovay-Kitaev定理证明思路 来源：“Quantum Computation and Quantum Information”

通过这样的方式，Solovay和Kitaev证明逼近任意单比特态只需要Θ(log^c(1/ϵ))个基础门，其中c≈4。而对于m个任意单比特门组成的电路，则只需要Θ(mlog^c(m/ϵ))个基础门。这只带来了对数级的额外代价，自然是完全可以接受的。

两比特门

经典的逻辑电路基于布尔代数，而布尔代数是通过与、或、非运算定义的。相应地，所有的逻辑电路只需要这三种门就全都可以实现了。事实上，借助非门，与门和或门是可以互相替换的。这样一来，只需要与、非，或者或、非门就够了。人们甚至把它们各自组合在一起，构成与非门和或非门，并称它们为通用门。

那么，在量子电路中，我们还需要哪些两比特门，才能与基础的单比特门一起构成一组通用门集呢？当然，这里的通用是在近似的意义上说的。答案很简单，只需要一个就够了，那就是受控非门，CNOT。

单比特门可以借用Bloch球面来直观地定义，两比特门定义起来稍微麻烦一点，不过在物理上可以轻易解决这个问题。

所有门的定义都必须跟式（1）那样的态叠加相容。换句话说，我们可以利用态的叠加性将门的定义约束到经典比特态上。于是，对于这里的CNOT门我们只需要定义它的经典版本就可以了，如下图：

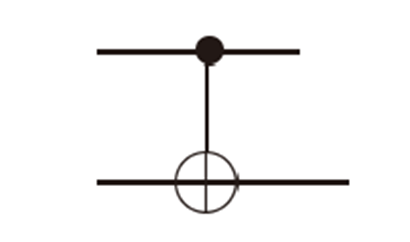
受控非门CNOT

这个门分为两个部分：首先将上面的比特复制一份，然后跟下面的比特做模2加法⨁。

有了CNOT门，我们就可以声称：{H,S,T,CNOT}构成一组近似通用门集。也就是说，任何n比特门都可以通过它们的反复作用来近似地实现。

要证明这一点有点繁琐，我们只给一个定性的说明。一个任意n比特门包含两方面：在每个比特上的作用，以及比特之间的关联，或者说量子纠缠。利用CNOT门可以实现两比特之间的纠缠，而不断地在各个比特对之间作用CNOT门可以实现任意的n比特纠缠。一个简单的例子是三比特的Toffoli门，也叫控-控-非门，或者量子与门。它的一种实现方式是：

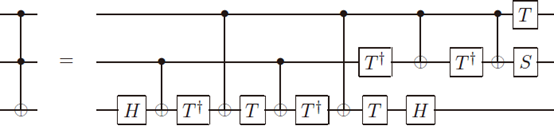
Toffoli门的实现 来源：“Quantum Computation and Quantum Information”

这里的T†是T的逆，也就是绕z轴转动-π/4角度。

不过，通过这种方式来实现多体纠缠是非常低效的。我们可以简单地估算一下逼近一个任意n比特态所需要的的门数目。类似于Bloch球，n比特态可以用一个（2ⁿ⁺¹-1）维空间中的球面来表示：

逼近一个n比特态，摘自“Quantum Computation and Quantum Information”

如果想要以精度ϵ逼近球面上的点，我们需要用半径ϵ的圆盘去覆盖整个球面。在（2ⁿ⁺¹-1）维空间里，可以计算出这个覆盖需要的圆盘数是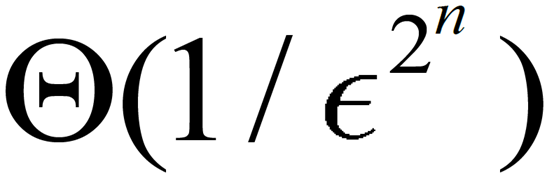。而要得到这么多的圆盘，我们需要大概Θ(2ⁿ)那么多的门。这当然大大超出了我们的承受能力。

由此我们得出结论，绝大部分n比特门都是量子电路难以有效实现的，而我们在编程时应选择那些易于实现的。同时，这也引发了一个新的概念，也就是量子计算复杂度，以及相应的量子版本的P与NP问题。而这些结果和概念又会进一步体现在量子多体系统的性质和分类中，这里不再详述。

有朋友可能看出来了，在我们的近似通用门集{H,S,T,CNOT}里面，S其实是多余的，因为S=T²。但人们仍然习惯保留S门，因为{H,S,CNOT}构成了一类非常特殊的电路，Clifford电路。

简单来说，这种电路会让每个量子比特都“等效地”处在某个坐标轴上，也就是准经典八面体的顶点上。正因为这一点，Clifford电路可以用（概率型）经典计算机有效仿真，这就是所谓Gottesman-Knill定理。

Clifford电路因为其特殊性，有着极为广泛的应用，我们之前曾经提及过一些，以后有机会再详细讨论。